SOMMAIRE :
- sujet du DL
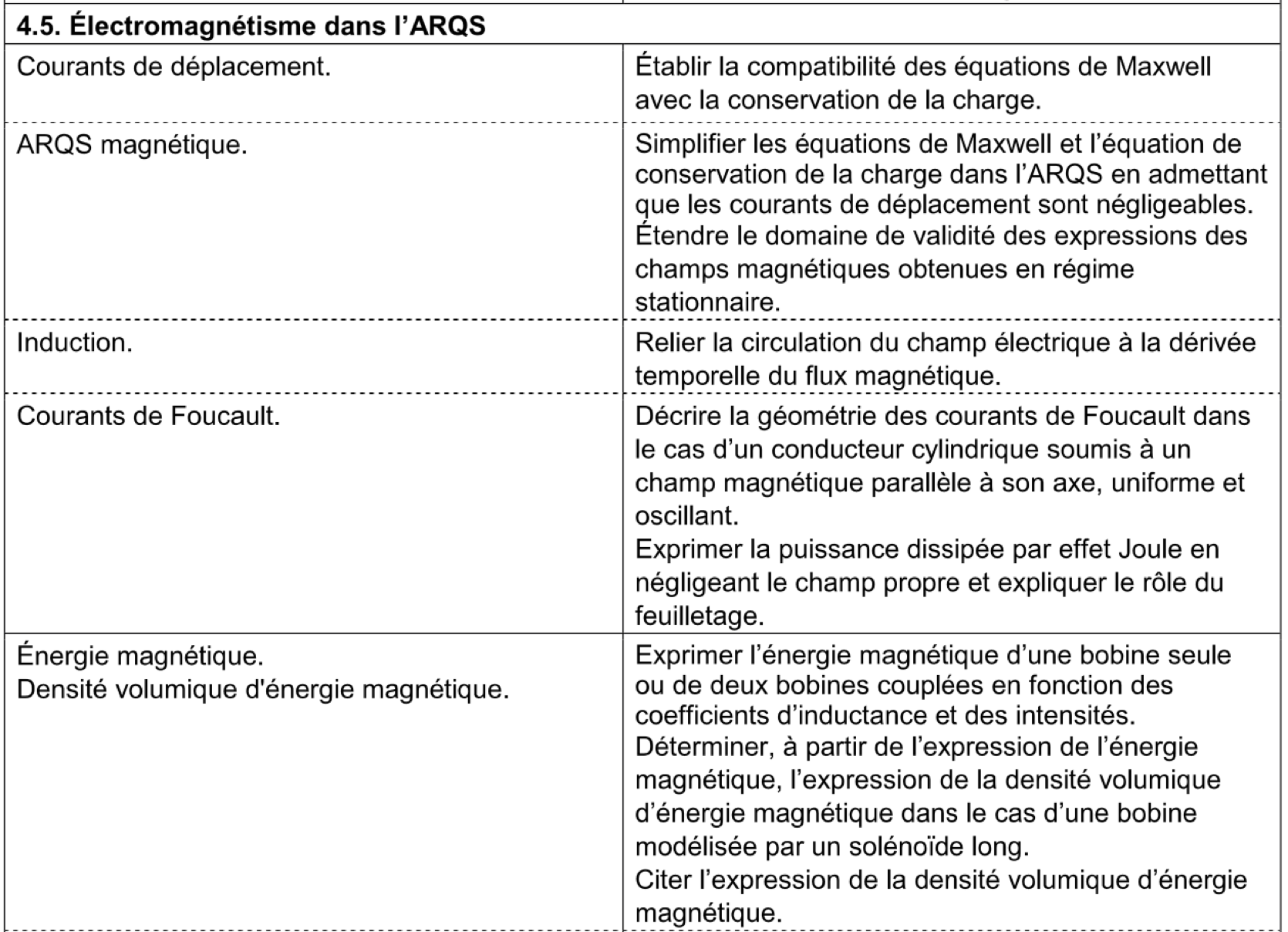
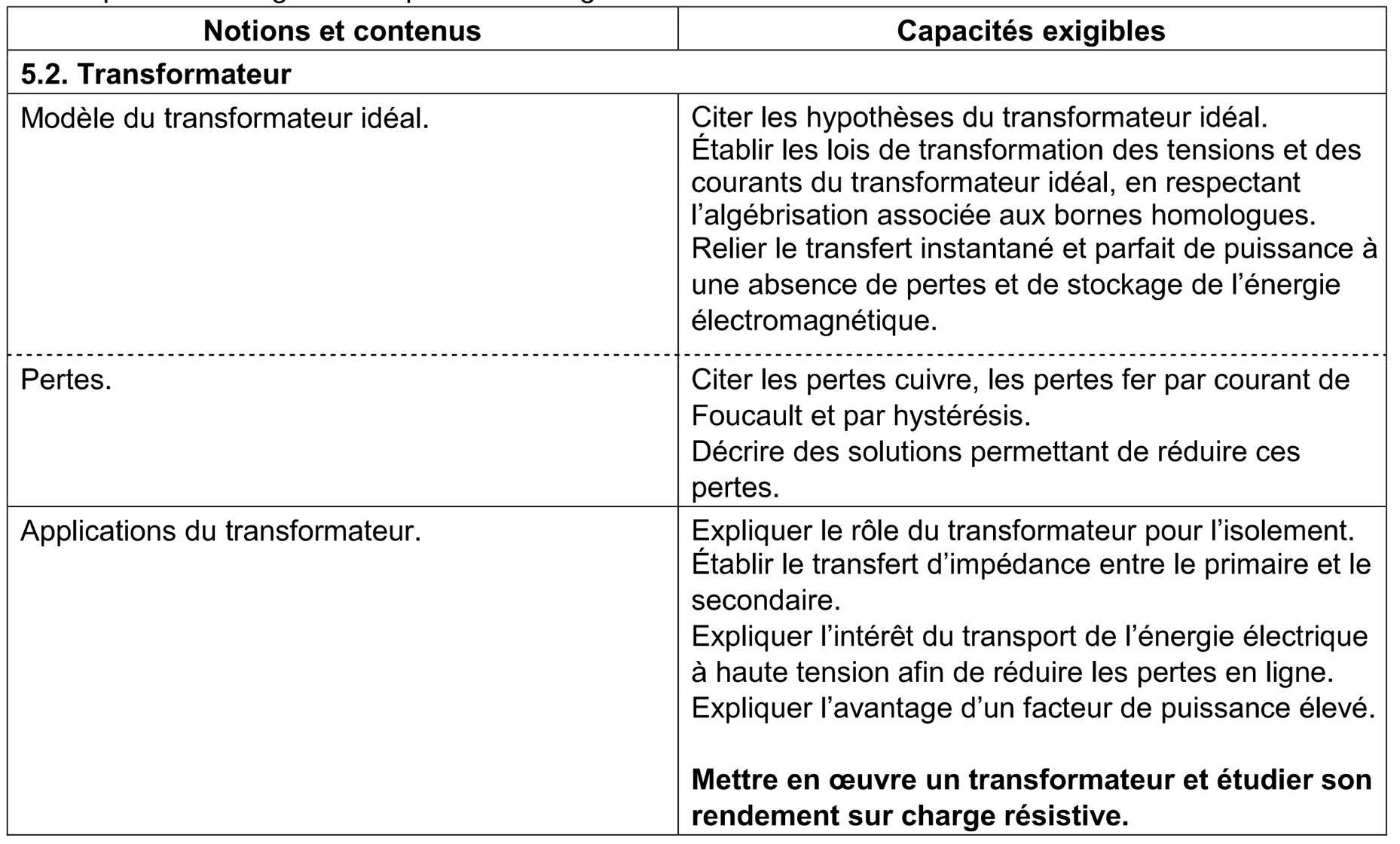
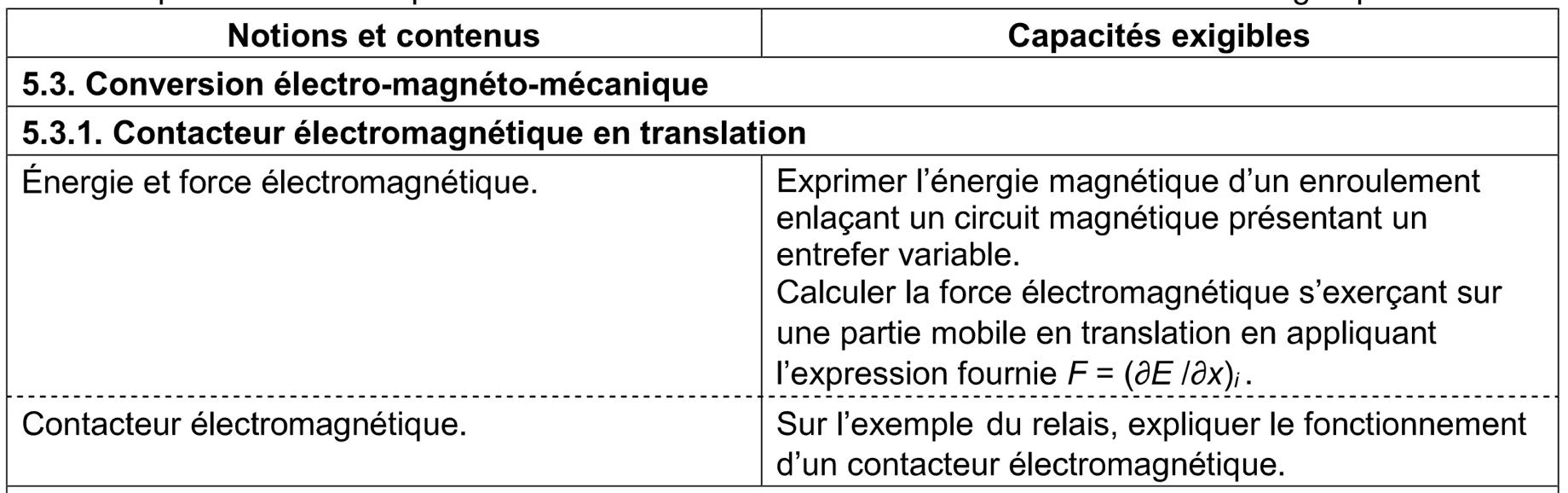
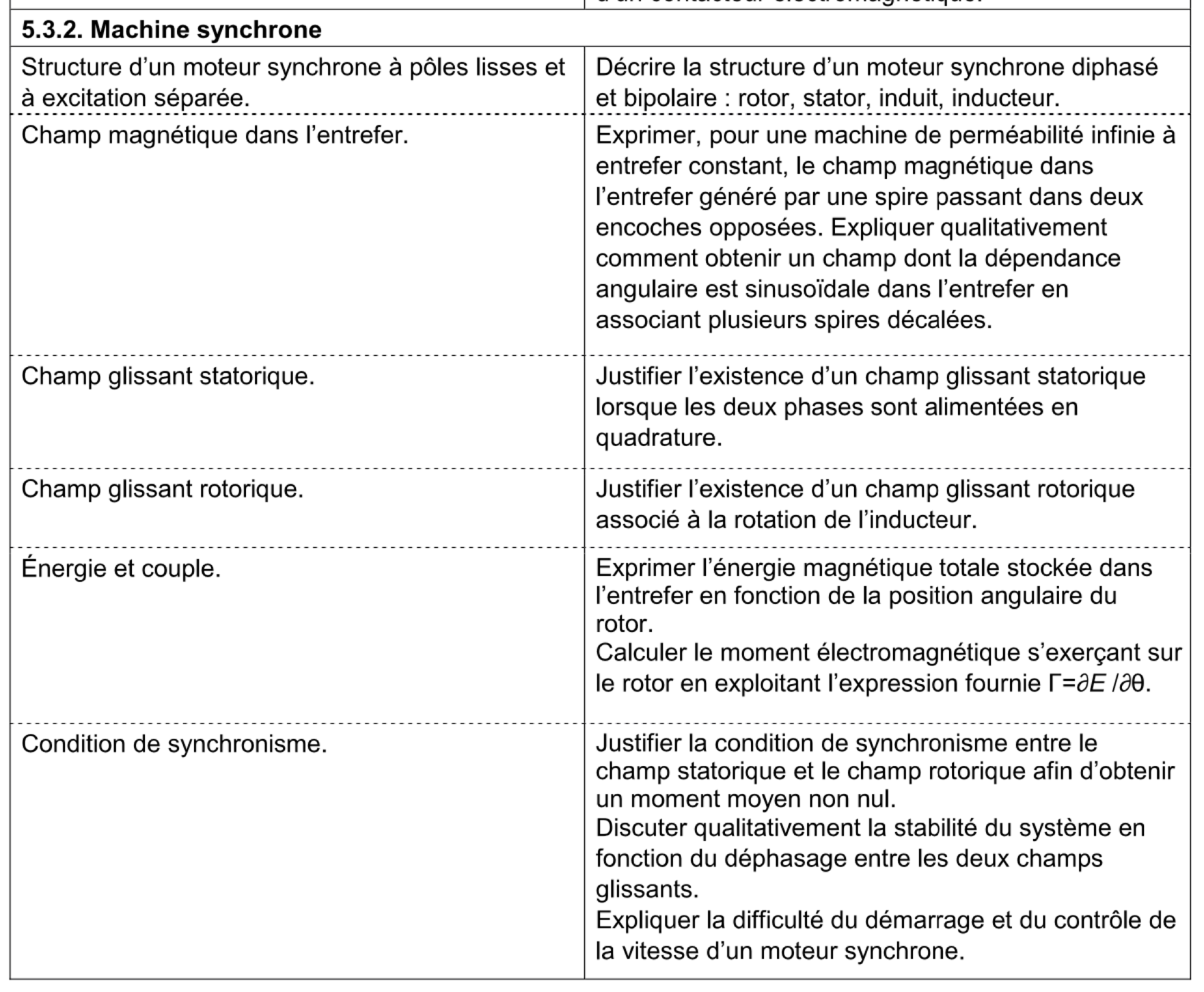
- programme officiel
- programme de colle 13
- planning de la semaine
- images MCC
- magnéton de Bohr
- HACHEURS
- Photos TP hacheur
- exercices
WebMaster : O.GRAS
Enseignant Sc. Physiques CPGE spé PSI
Création du site :1er juin 2020
Mise à jour : 25 juin 2025
Objectifs
À rédiger pour vous (pas de rendu) =
Devoir pour la rentrée + un sujet optionnel PSI*
Les corrections seront données en milieu de semaine prochaine
REVISIONS : CRISTALLO et PROBLEME A DEUX CORPS (Sup)
Interro à la rentrée, sur le programme de révision (hacheurs)
Rentrée : Bilan des voeux d’inscription aux Concours (voir plus bas)
Rentrée : Rédaction MCOT et avancement du TIPE afin de pouvoir repositionner chaque sujet (voir plus bas)
JOYEUSES FETES DE FIN D’ANNEE
Semaine calendaire 52 du 23 au 29 décembre 2024







Hors colle
Hors colle
Théorème de Ferraris

Chimie, notion de potentiel chimique



Lois de Le Châtelier
Programme de colle

Programme 13 de colle de Physique-Chimie :
SAVOIR :
—chimie : identités thermodynamiques (dH, dG), expression de S en fonction de la dérivée de G par T, relation de Gibbs-Helmholtz, dG négatif démontré pour une réaction spontanée, potentiel chimique et enthalpie libre molaire, identité d’Euler, relation de Gibbs-Duhem, volume molaire et entropie molaire en fonction des dérivée du potentiel chimique, démonstration : la quantité d’une espèce diminue si son potentiel chimique est plus élevé + idem pour l’action de la pression ou le sens des échanges thermiques. Equilibre = égalité des potentiels chimiques + activité d’une espèce (gaz, liquide, solide, solvant) + enthalpie libre standard de réaction à l’équilibre.
+ lien entre la constante de réaction de l’enthalpie libre de réaction, relations de Gibbs-Helmholtz + détermination de l’avancement + quotient de réaction Q , prévision du sens d’évolution d’une réaction par le rapport K/Q + lois de Le Châtelier
— dipôle électrostatique p : expression du potentiel V et du champ E (8bis)
— ARQS : loi de conservation de la charge, les 4 équations de Maxwell, équation de Maxwell Gauss pour calculer un champ E avec l’expression de div(), équation de Maxwell Ampère pour calculer un champ B avec l’expression de rot()
- équations de Maxwell : loi de Lenz-Faraday, champ magnétique imposé dans un isolant par un champ E extérieur sinusoïdal, rappel des rails de Laplace avec résistance + cas avec une bobine, relations de passage pour E et B données, loi de Lenz et tension aux bornes d’une bobine idéale + notion d’inductance L, cas de l’induction pour une spire tournante dans B fixe, effet Joule microscopique, courants de FOUCAULT (calculs pour un cylindre et puissance dissipée par effet Joule) + cas des plaques à induction de la cuisine.
- vecteur de Poynting, cas de la résistance cylindrique, énergie volumique électromagnétique (Pas encore les définitions complètes de L et de la mutuelle M)
- milieu magnétique : cycle d’hysteresis + pertes par hysteresis, champ rémanent, champ coercitif, effet mémoire, définition de H et M + le cas idéal (cours et TP) du transformateur avec relations en tensions et courants + adaptation d’impédance.
- Circuits magnétiques : théorème d’Ampère, notion de réluctance R, de flux magnétique et loi de Hopkinson (semblable à la loi d’Ohm), associations série et parallèle de réluctances, notion d’entrefer et de champ amplifié dans le matériau et/ou dans l’entrefer, analogie avec les ALI.
- Moteur synchrone : expression du couple exercé sur un dipôle magnétique soumis à un champ B tournant, champ tournant créé par une bobine ou deux bobines alimentées en courant sinusoïdal. Energie dans l’entrefer : parfois donnée et calcul du couple ensuite.
- HACHEUR série (dévolteur) : cours et exemples sur le bloc de deux interrupteurs, lissage par une bobine, cas du courant i sans interruption, modèle à haute fréquence linéarisé, établissement du courant dans R et des pentes à partir des équations différentielles selon l’intervalle de temps (en fonction du taux de hachage \alpha), utilisation des pentes pour établir l’expression de la fluctuation de courant, utilisation de la tension moyenne nulle aux bornes de L pour démontrer l’expression de la tension moyenne aux bornes de R
- Hacheur parallèle, pont de 4 diodes, onduleur à 4 interrupteurs.
Questions de cours pour la colle
Les 6 questions de cours :
1-
2-
3-
4-
5-
6-
Physique-Chimie-TIPE- TP-Python
Vidéo sur le fonctionnement d’une MCC
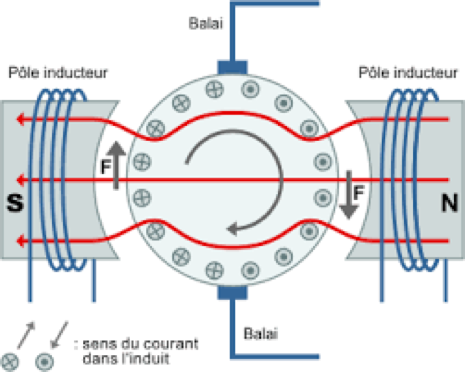

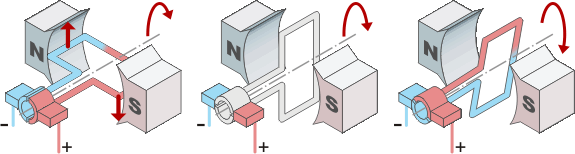
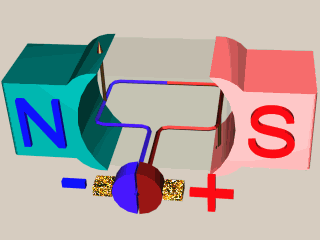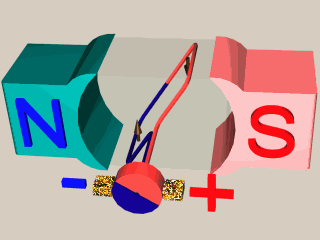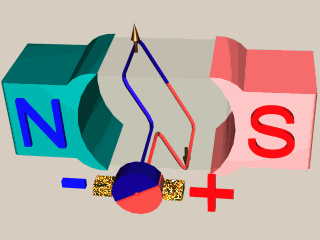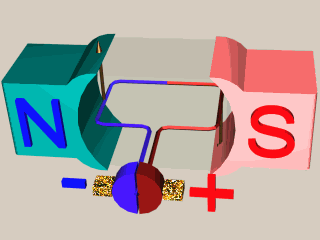
Fonctionnement du système collecteurs-balais

Balais

MCC : résumé des « soucis » de signes que l’on peut avoir en électromécanique
Compléments :
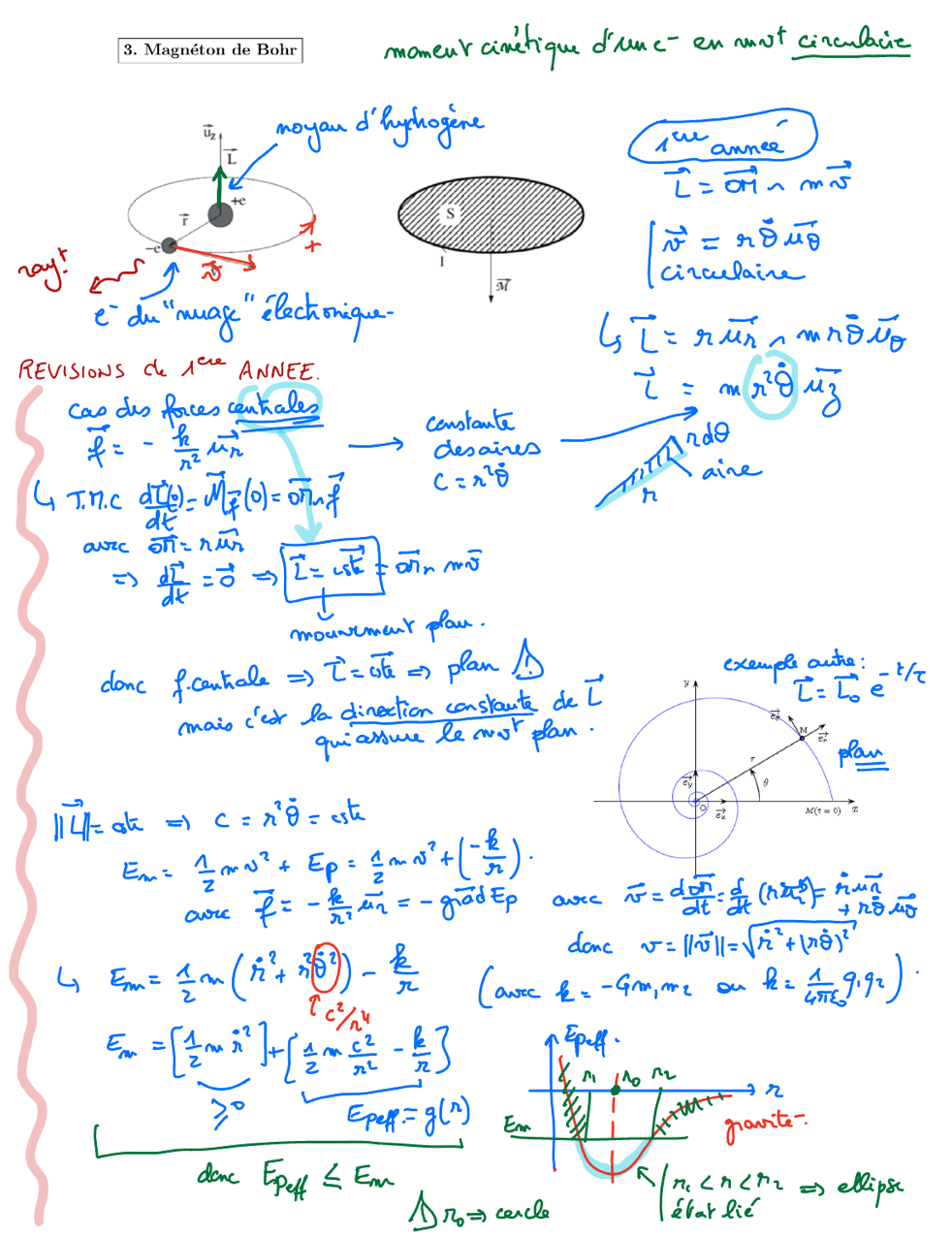
Attention : on a donc ici le début de révisions nécessaires sur la mécanique des pb à deux corps (trajectoires dans un champ de pesanteur, trajectoires circulaires)

Magnéton de BOHR : quantification du moment dipolaire magnétique.
C’est la partie élémentaire du 1er terme de la somme qui définit le moment magnétique total d’un atome :





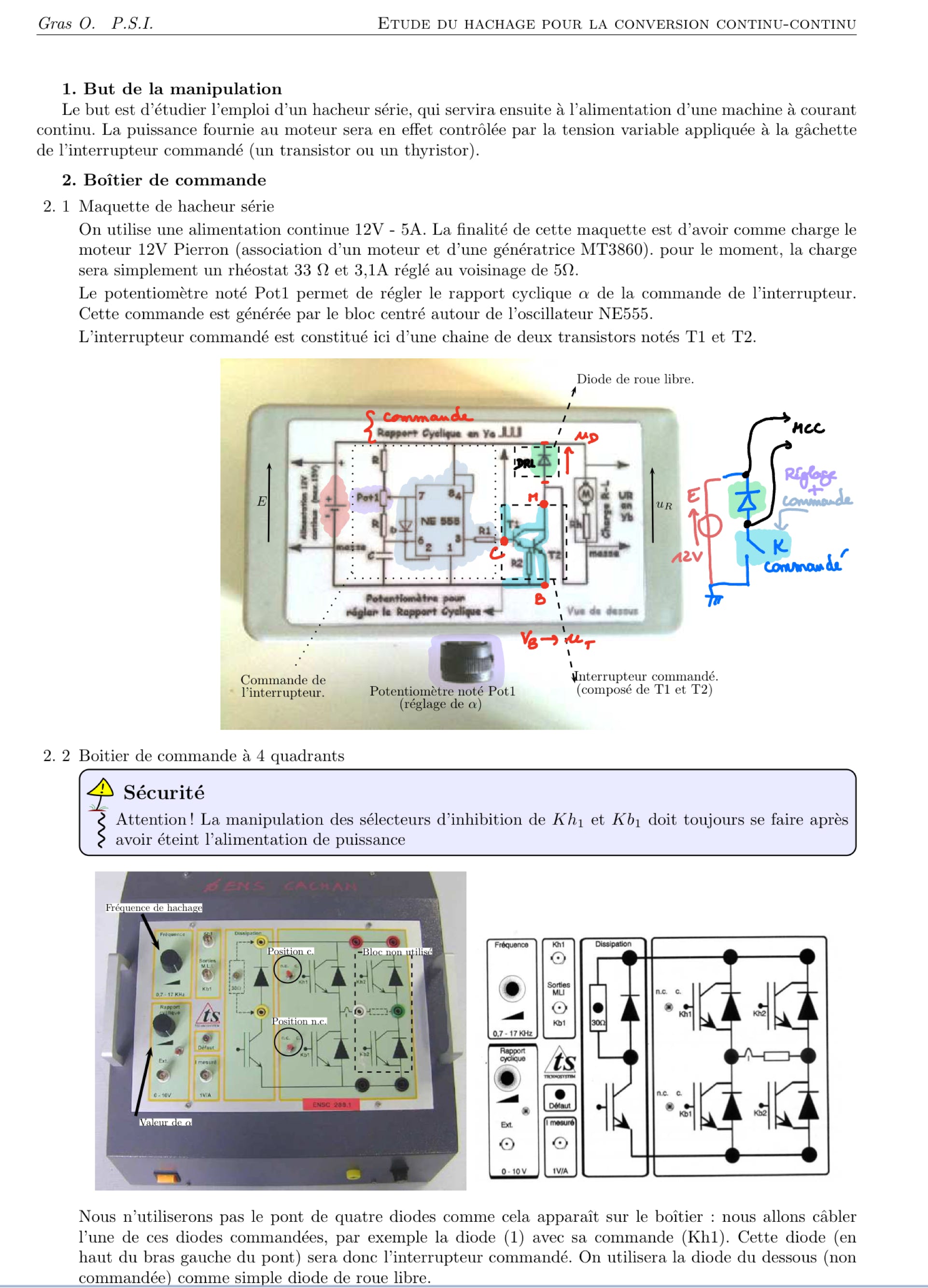
TP sur les hacheurs :
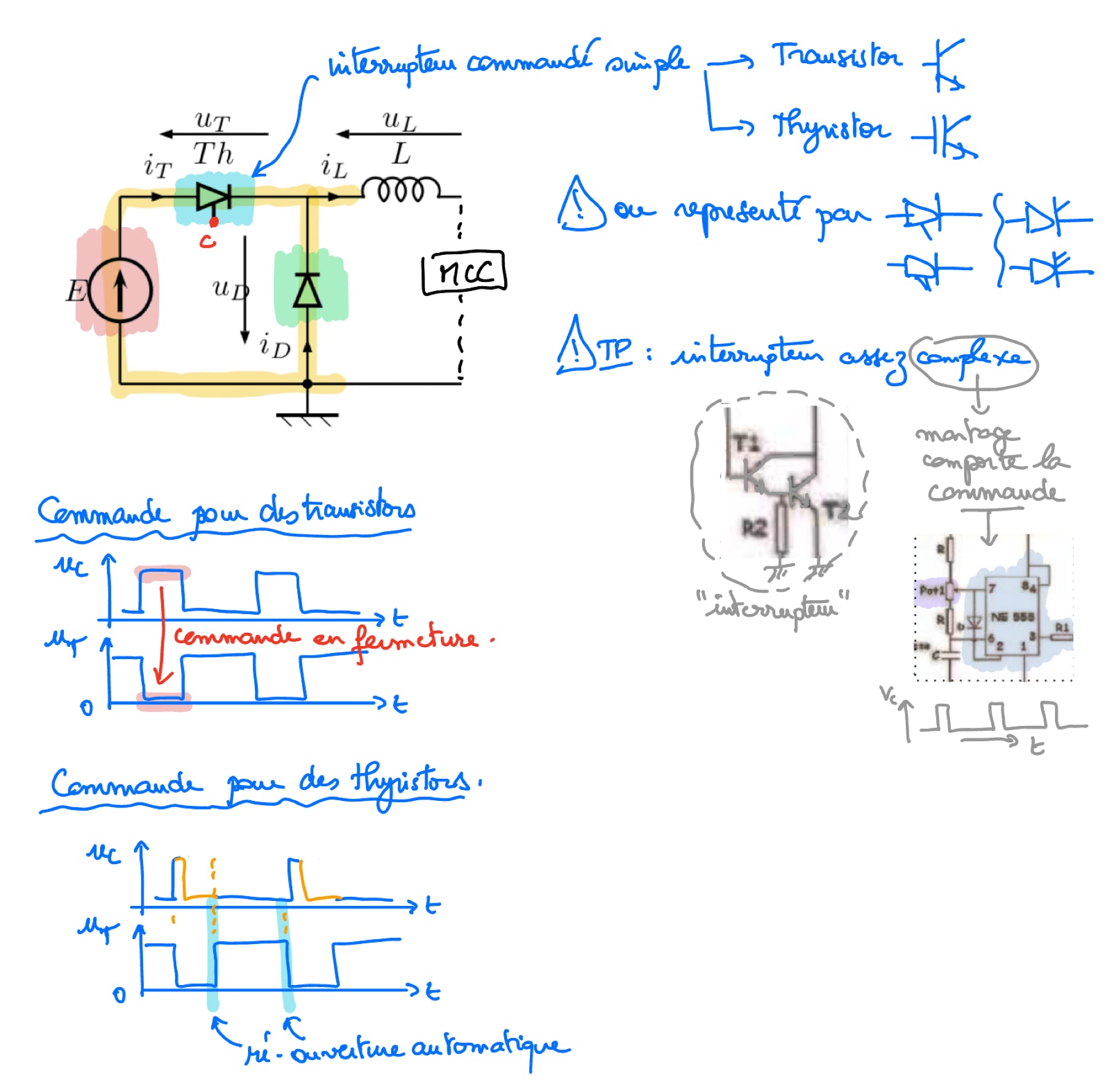

Courbes établies en régime transitoire :

Commande de l’interrupteur commandé
—————— Régime transitoire ——————————
—— Régime ——
permanent
Tension aux bornes de R
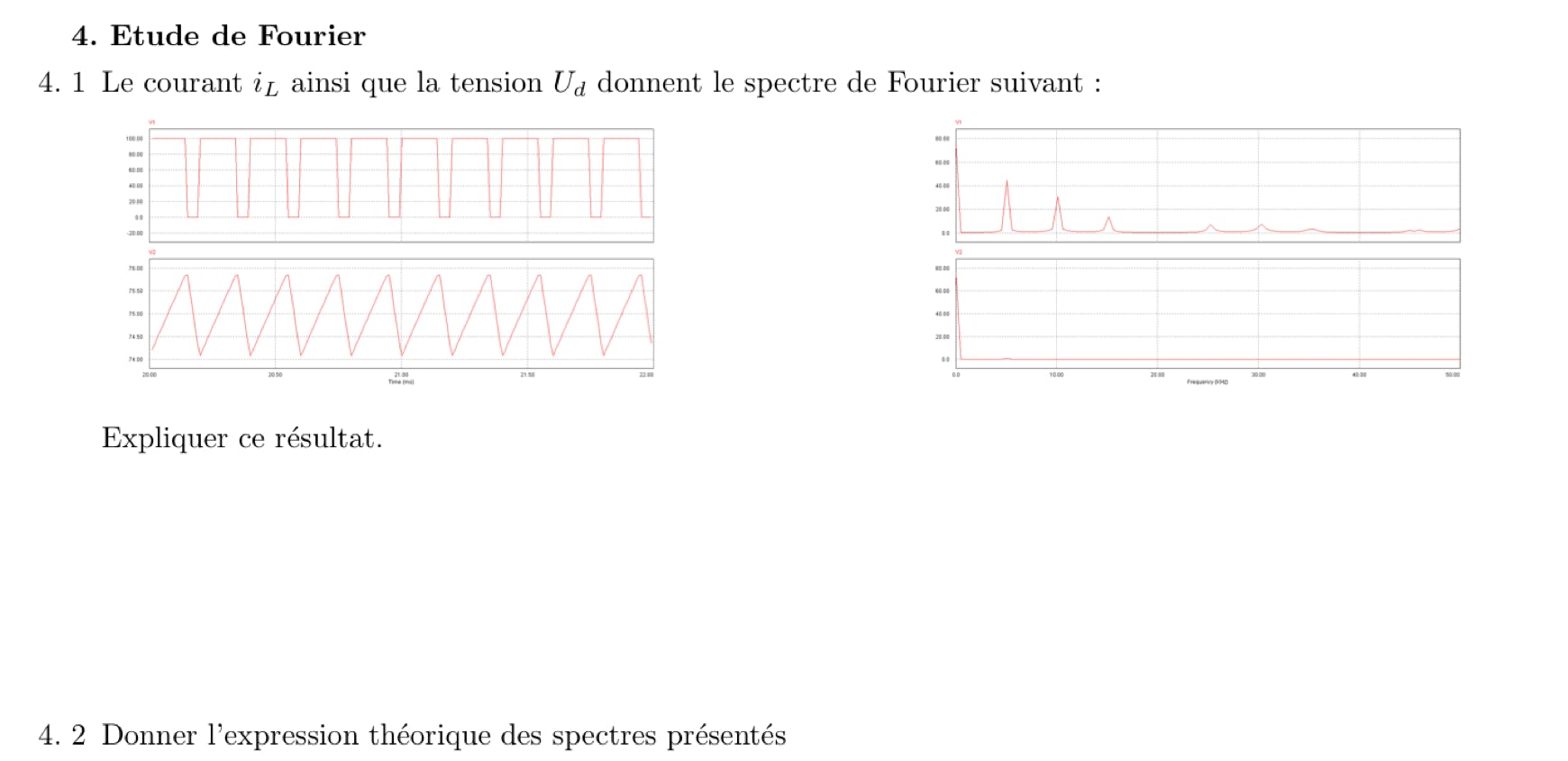
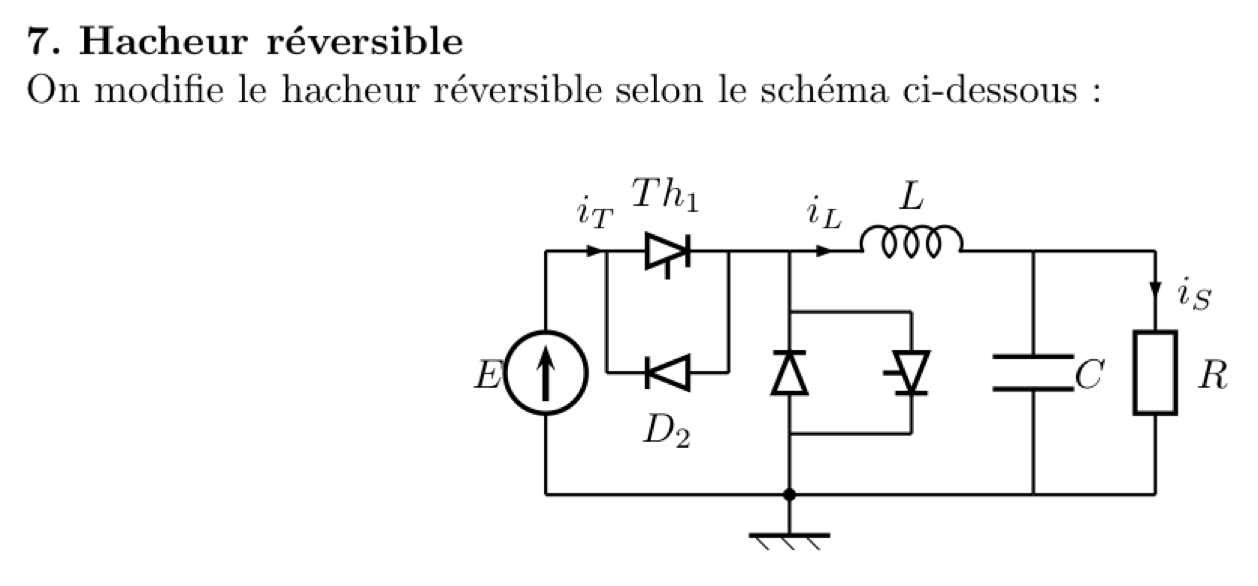

Boitier à 4 interrupteurs couplés à des diodes

Montage de hacheur série en TP
Bobine de lissage en détournant un transfo


(Jaune) tension u(R) : but non atteint
Lissage de i(R) : une bobine dans le 1er cas

(Jaune) tension u(R) bien lissée
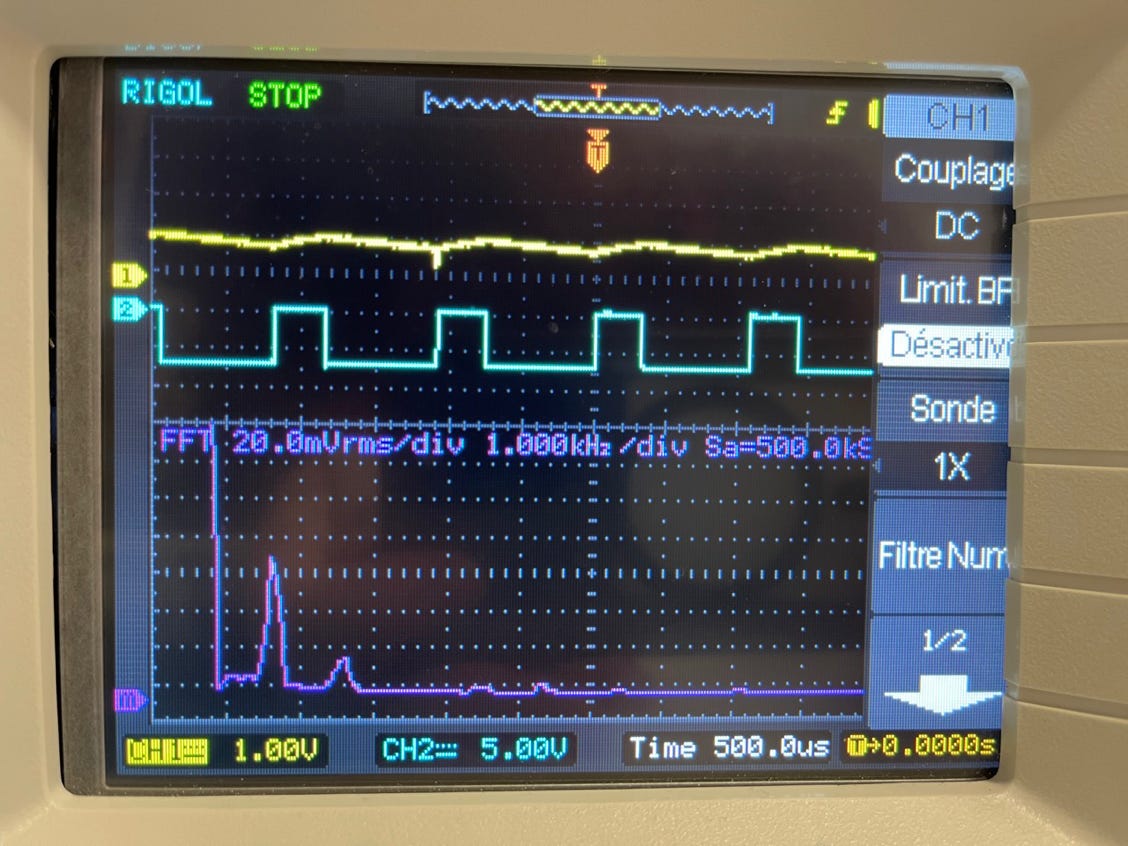
Lissage de i(R) : 2 bobines en série + matériau = L plus grand

(Bleu) : commande, on y voit bien la valeur de \alpha
(Jaune) : tension u(R), on a ici une tension comme dans le cours avec une valeur moyenne non nulle, des parties linéaires (et non exponentielles). Le spectre de Fourier (1er pic élevé, hors cadre) montre que les ondulations sont faibles par rapport à la composante continue.
(Jaune) tension u(R) bien lissée et zoomée (voir le zéro)

Exercice sur les MCC (extrait d’un sujet)


Attention au signe du moment : ici, c’est le choix
— Deux façons de faire ensuite : on peut utiliser les résultats de 1ère année, avec les rails de Laplace où la fem créée aux bornes de la barre mobile était
Attention au schéma électrique : entre C et D, on n’a plus que la fem e ici car on néglige dans l’énoncé la résistance et l’inductance propre L du rotor. Et on oriente ici e dans le sens du courant i d’où un changement de signe sous-entendu.

Attention : le cadre tourne dans le sens opposé à la règle de la main droite et l’axe des z !!
et ici la vitesse n’est plus rectiligne mais curviligne (rotation des barres MN et OP de la spire) donc pour chaque barre on écrit :
Ce qui donne pour les deux barres :
— Deuxième façon de faire : on peut faire le bilan de puissance. Si le rendement est de 100%, la puissance électrique fournie est égale à la puissance mécanique en valeur absolue :
Ce qui donne pour l’expression de la fem :
— Troisième façon de faire : on pouvait dans l’ancien programme utiliser un « champ électromoteur » et vous verrez cette méthode dans beaucoup d’anciens exercices (et il suffit de remplacer par une des deux méthodes précédentes) :

———— Résolution ————
———— Equations mécanique et électrique ————


Attention : on projette sur l’axe des z !! Donc cette équation fait tourner dans le sens opposé




Attention : on projette sur l’axe des z !! On voit que la vitesse angulaire limite est négative, ce qui nous fait retrouver le sens réel positif de rotation !
Attention au signe de la vitesse angulaire limite : ici, c’est le choix initial qui nous fait prendre des signes opposés à ceux du cours, mais c’est parfois imposé par les sujets de concours
Donc en résumé, pas d’étonnement à avoir dans certains sujets des changements de signe en fonction du sens de la fem e sur le schéma initial :





On voit donc que l’on obtient bien la même équation que dans le cas où le schéma a la fem e dans le sens opposé au courant (ce qui est plus « normal » puisque la fem s’oppose au courant du générateur u )
MCC : exercices et compléments

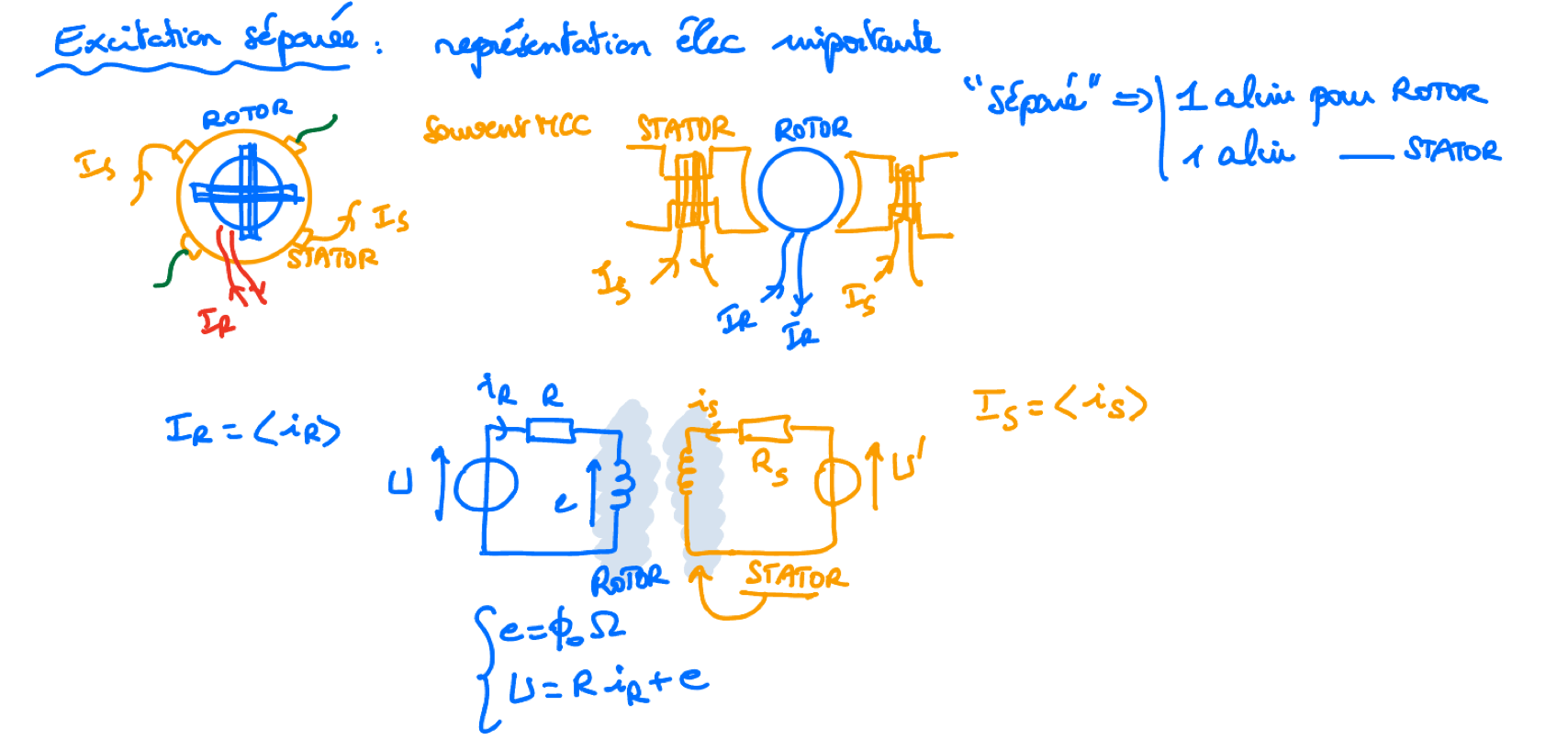
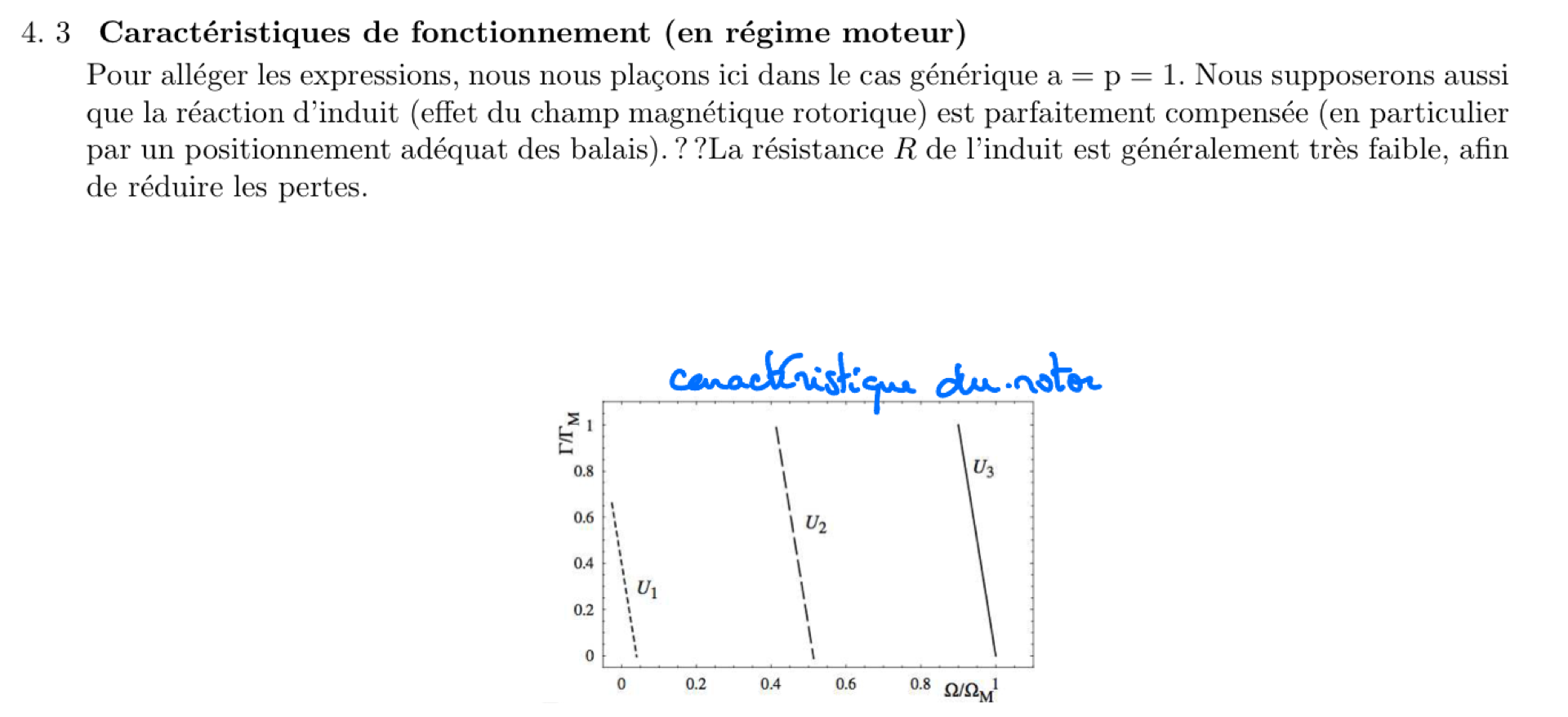
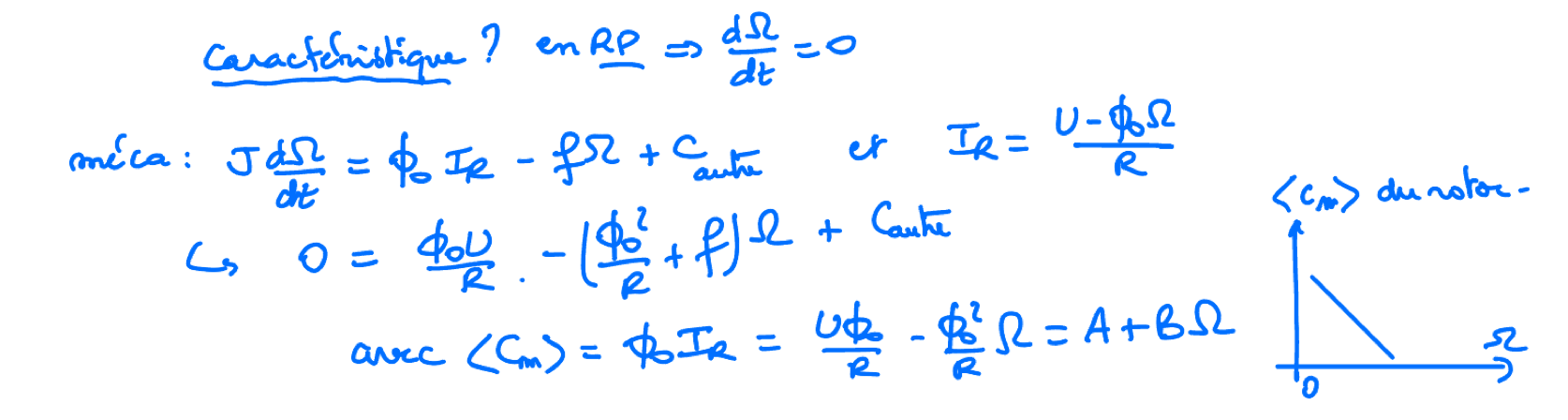







Autre analyse de l’équation différentielle du rotor en RP :


Si le stator n’est pas constitué d’aimants permanents, il y a donc forcément des bobines alimentées et le courant de ce circuit d’inducteur peut jouer un rôle important et SURTOUT être la cause d’un EMBALLEMENT du moteur si ce courant s’annule:





